Now we are going to start exciting 3D text design how to design 3D text by Photoshop Software. There is no alternative way to learn 3D text without tutorial so let’s start to learn 3D text design depend on tutorial.This tutorial will teach you how to create and style a 3D text in Adobe Photoshop. Using this tutorial.
Tutorial you will learn not only how to create great looking 3D texts in Photoshop but also any kind of 3D object. Work with any Photoshop version. I have already created an action for Graphic River that basically does the same thing, but you can’t really customize that one unless you have some more knowledge above this tutorial.
Anyway, following this tutorial, you will have full control over the results – specially the perspective angle and height of the text. You can also check out the PSD file included to see the how the 3D text looks and take a look at the Blending Options.

Step# 1
We’re going to start by making a new design, at first take new page like this, 1024×768, 72 dpi. Here we’re going to make a text layer. Black to be visible on the white background, but the color doesn’t really matter as we’re going to change it later. An Arial Bold, 180 pt sizes would be good. My text has a tracking of 100, so there’s a little space between the letters, but that’s not important either.
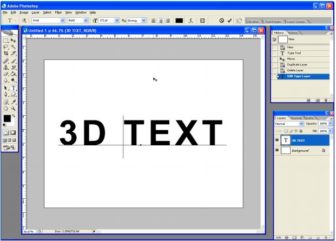
Now we will add a perspective look to the text so that it will look like standing on a flat surface. First we must rasterize the text layer. Right-click on the text layer in the layers panel and select.
Rasterize type…
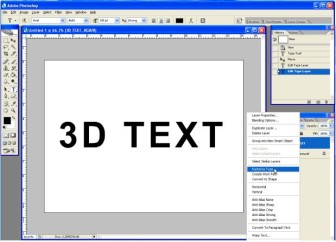
The text is not going to be editable now, but we are able to add perspective to it. Go to Edit –Transform – Perspective. A container for the text will appear. Click on the left corner (or right one) and while holding the click button, drag it inside, towards the center, until you see an H: angle value of around 40 in the transform toolbar.

Then, without hitting Enter or OK, go again to Edit – Transform and select Scale. Now, click on the upper middle control point and drag it down until the H: value is around 60%. Hit enter or the OK button.

Step# 2
With the text layer selected, make sure the move tool on the toolbar is clicked (the arrow with a cross). Now holding down the ALT key (the Option key on the Mac), click on the keyboards up arrow many times. Each time you do so; a duplicate layer of the text will be made, and placed 1pixel higher above the older one. This way, we’ll construct the 3D look of the text. Do so as many times as you want. Around 30 times would be a good choice.
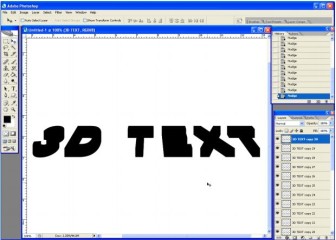
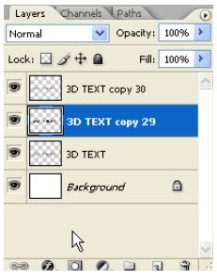
Now we have multiple layers, layer 30 being the last and topmost. Select layer 29, and while holding down the Shift key, click on the first copy of the text layer. This will select all the layers between the two.
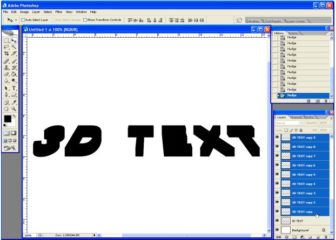
Now right click on any of these selected layers and select Merge Layers. This will combine all these layers into one that is the body of the 3D text.
So now we have 3 layers,
The topmost will be the “face” of the 3D text, the middle one will be its body and the bottom one will be its shadow.
Step# 3
As you see, our 3D text doesn’t quite look 3D-ish because it’s all black. So to make it look really 3D we’ll have to add him some colors and shadows. Gradients are what we need for colors because they will make this 2D text look like 3D for our eye. Shadows will improve it more, by creating the effect of text standing on a surface.
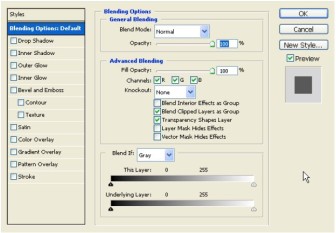
Let’s start with the bottom layer to add a shadow effect. This will create the look of the text as standing on surface. Select the bottom layer (3D TEXT is the name), right click and select Blending Options. The Blending Options Screen will appear.
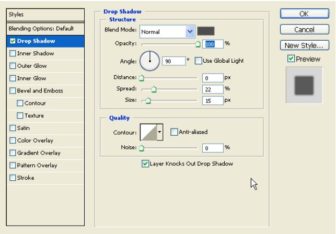
We’re going to add a shadow. Go to Drop Shadow and insert the values as seen in the image.
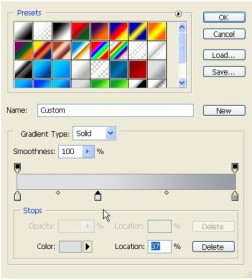
Now, we’ll move to the middle 3D Text layer. Select it, and then go to Blending options. We’re going to apply a gradient to emphasize the 3D look. Go to Gradient Overlay, use the settings shown.
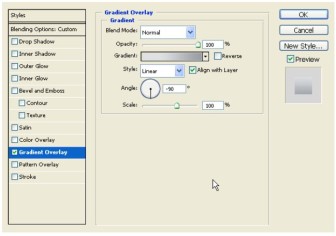
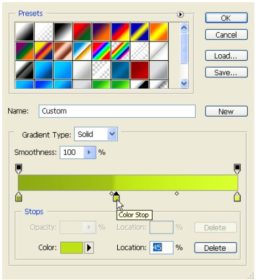
Click on the gradient and customize the color stops so that you start on the left with a light shade of grey and end in the right with a darker one. Click OK; apply the gradient and the blending options.

Here is our result by now.
You will notice there is a black bottom line around the text. That is because the middle layers starts 1px above the bottom one. So we’re going to fix this by raising the bottom layer 1px above. Select the bottom layer, click on the move tool from toolbar (if it’s not already clicked) and press the keyboards Up Arrow once. It will move this layer up by 1px.
Now we can focus on the top layer. Select it; go to Blending options – Gradient Overlay .
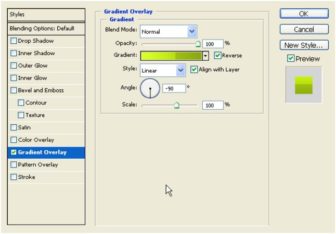
Click on the gradient. I’ve used the following # color codes for the color stops (double-click the color stop): Left one: 95a614, Middle one: c6dc1c, Right one: e2f936. If you don’t know how to add the middle color stop, it’s simple. Click just below the gradient. As you see, each color stop has 2 color midpoints. Position them like you see in the image.
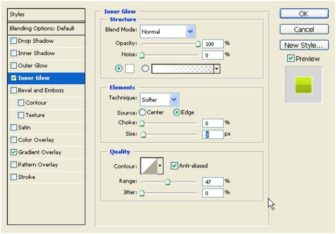
Now, to emphasize face of the 3D text we’ll add a small border (Blending options). You could do this with Stroke but I prefer an Inner Glow as you can control the hardness. Put the same values here as you see in the image.
Complete Our Design
Following this tutorial you will be able to create your own 3D text but also customize it the way you want. While there are actions available to the jobs, learning this tutorial will allow you to create various types of 3D text from various perspectives. Remember you can experiment with the first steps – the perspective and scale to produce different views.

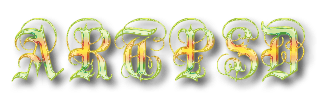

Shakil thank you very much for sharing with us Nice informative information about 3d text design in photoshop.i really like this article thanks a lot for this information